[10000ダウンロード済み√] ���等分線 辺の比 480367-二等���線 辺の比
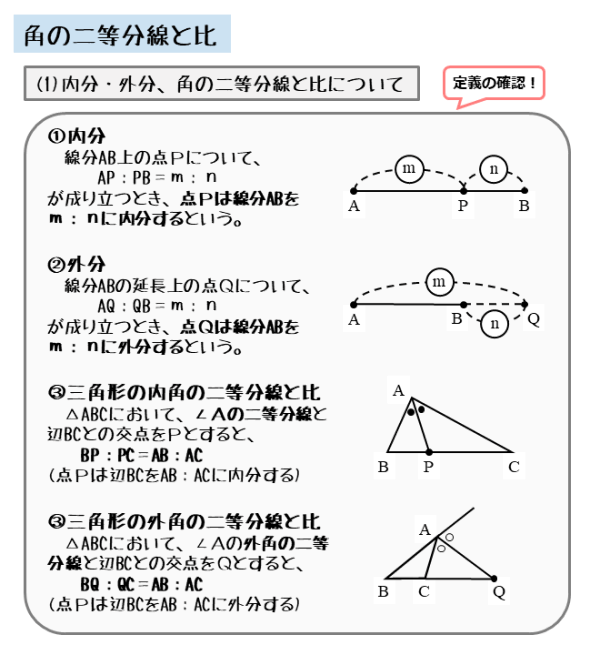
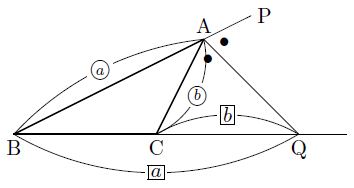
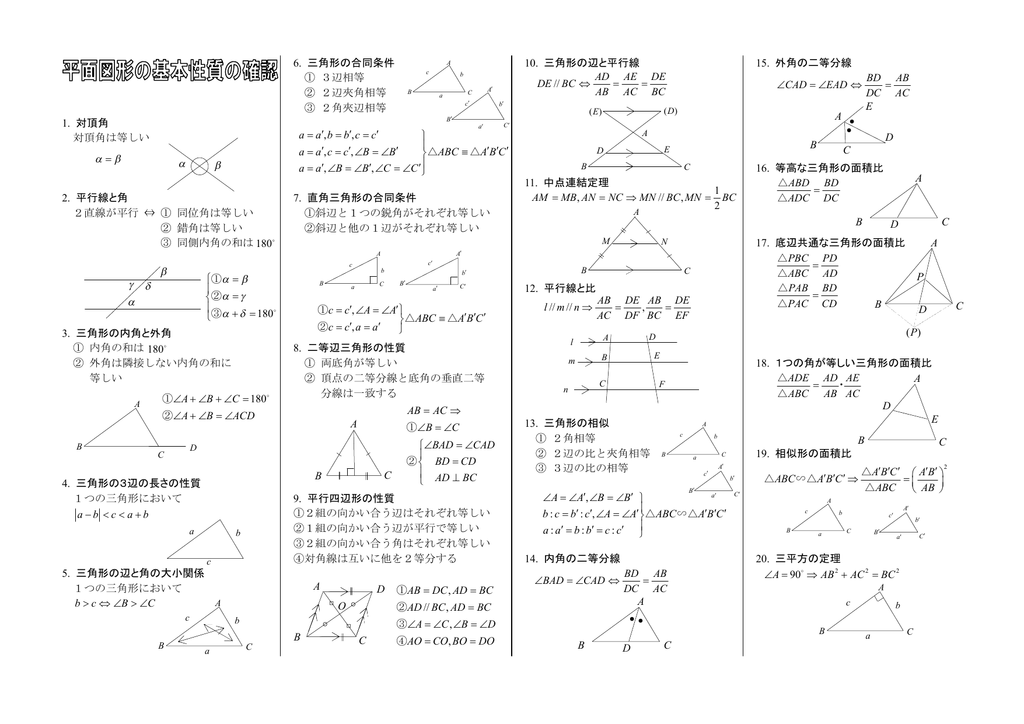
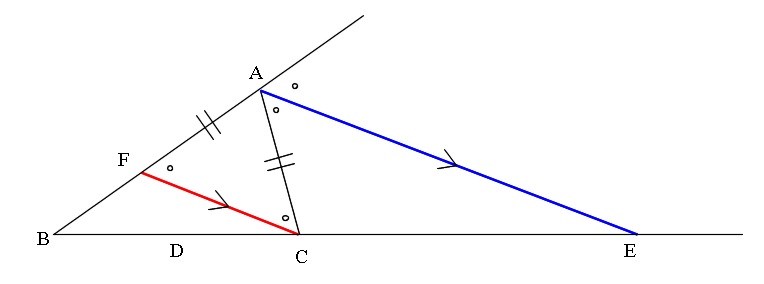
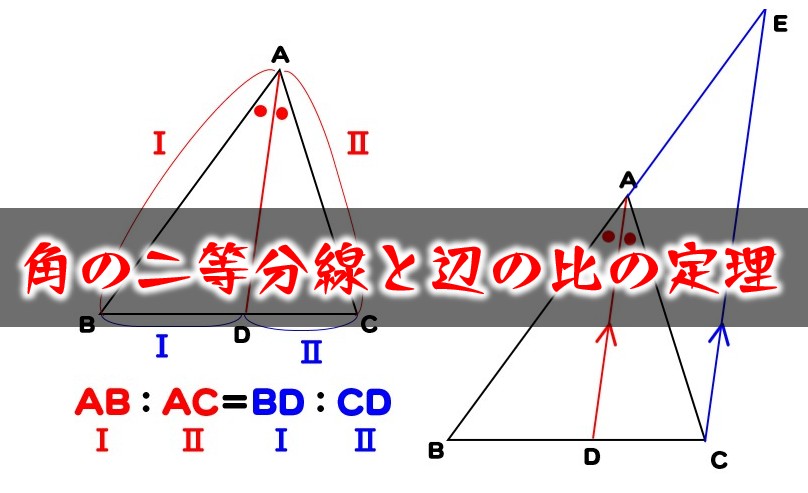
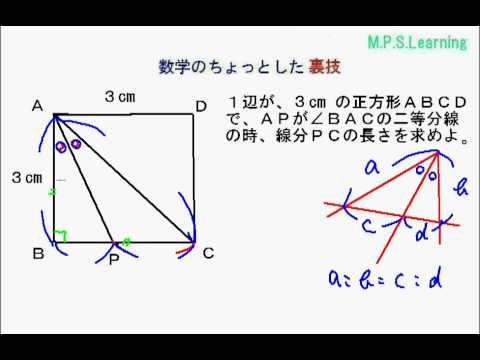
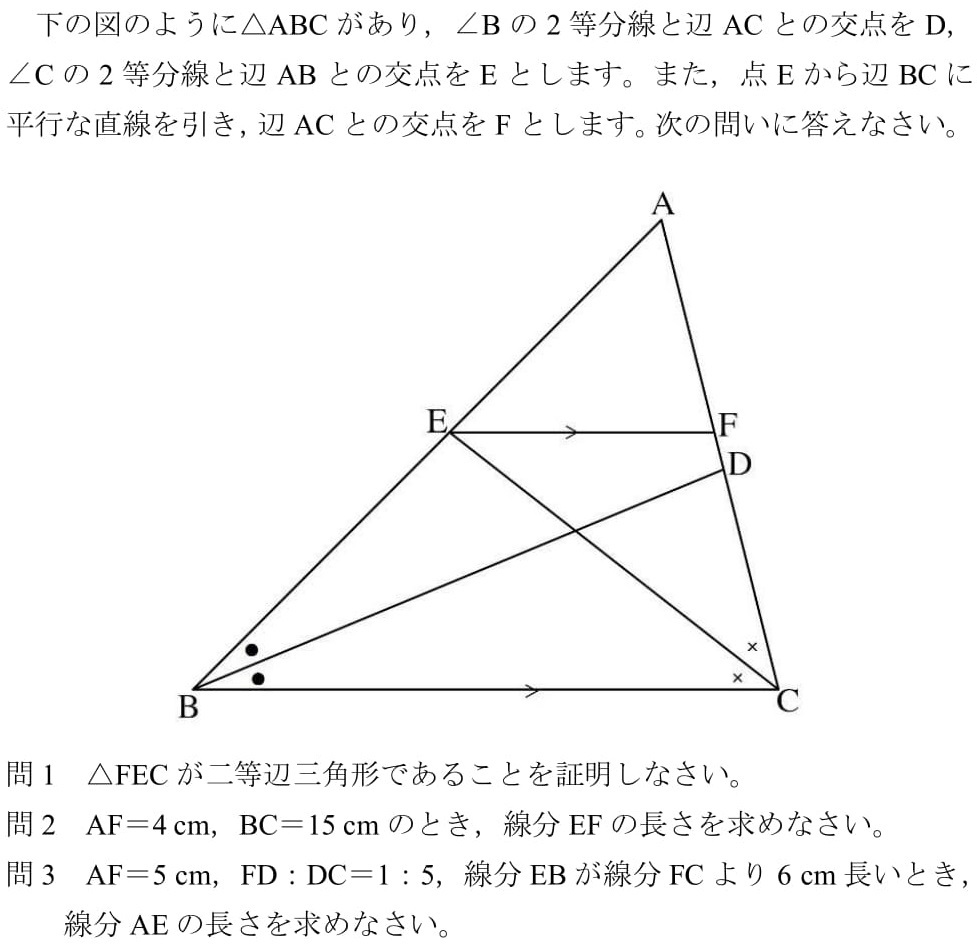
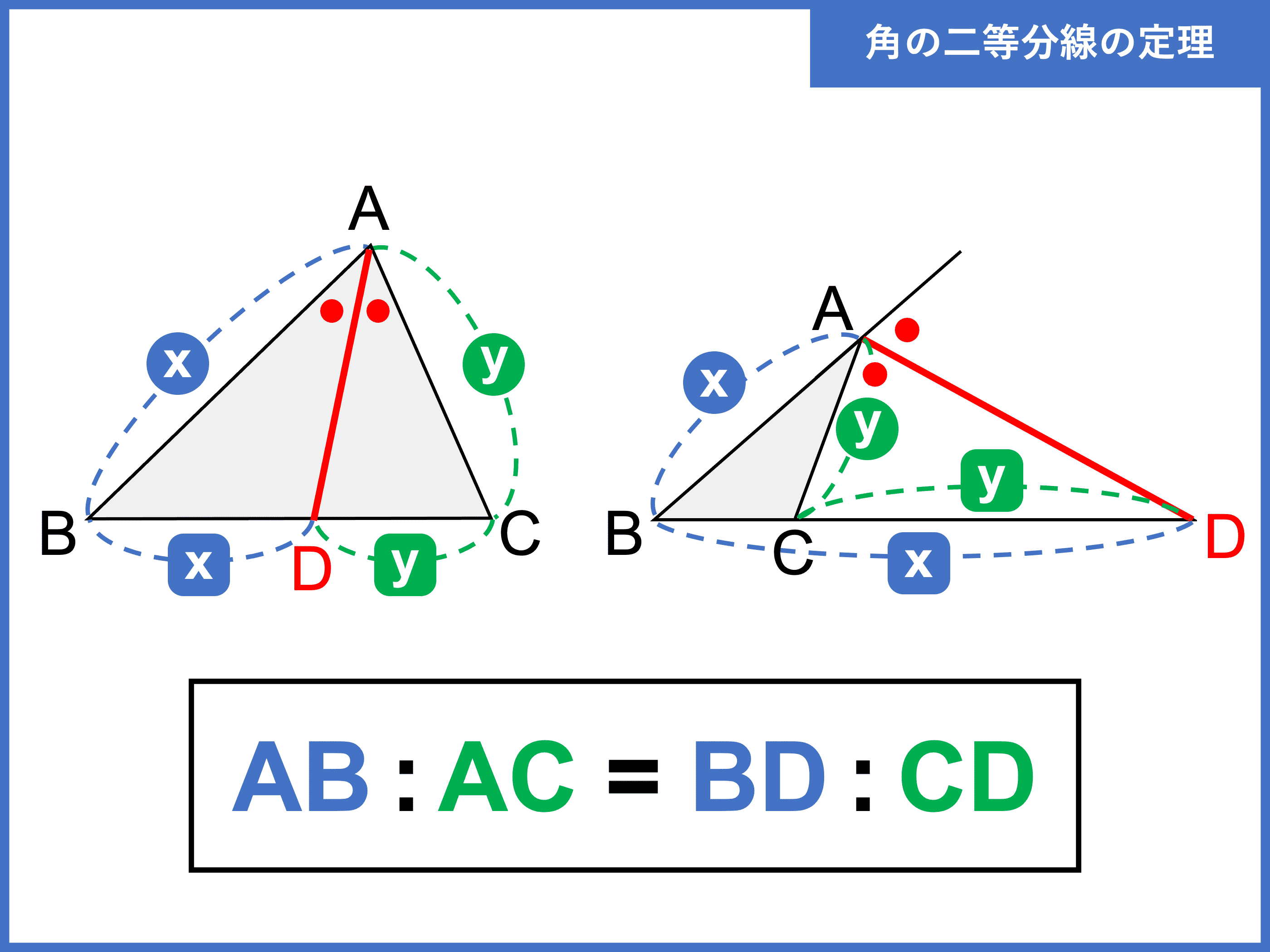
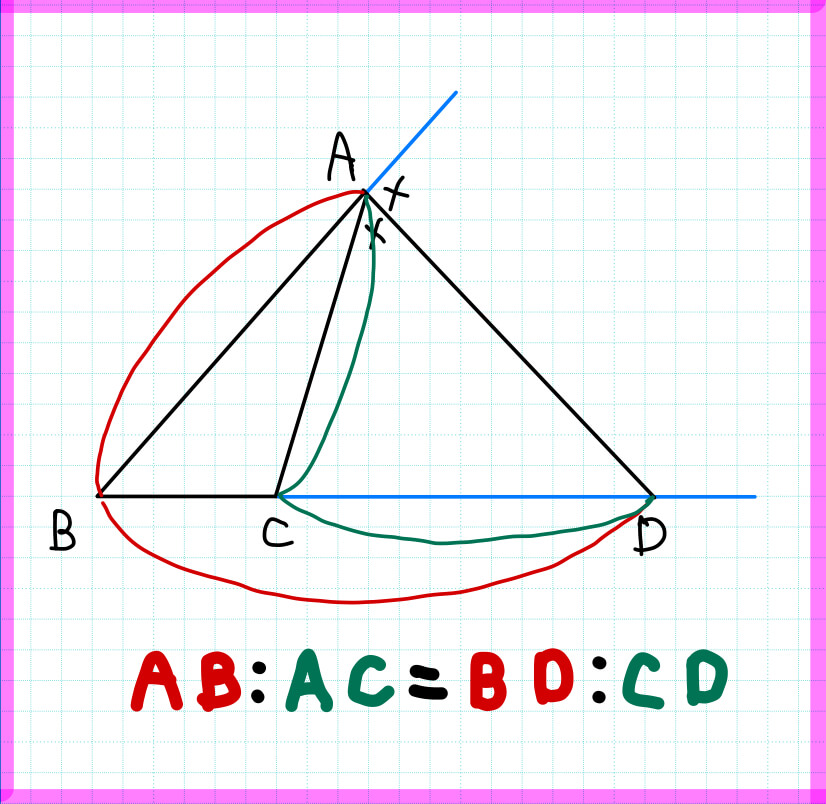
・内角の二等分線のある三角形の、等しい辺の比を、それぞれの形で見極めよう。 ・それが言える理由は、平行線と線分の比と錯角の利用 完璧じゃなかったら授業動画を見よう
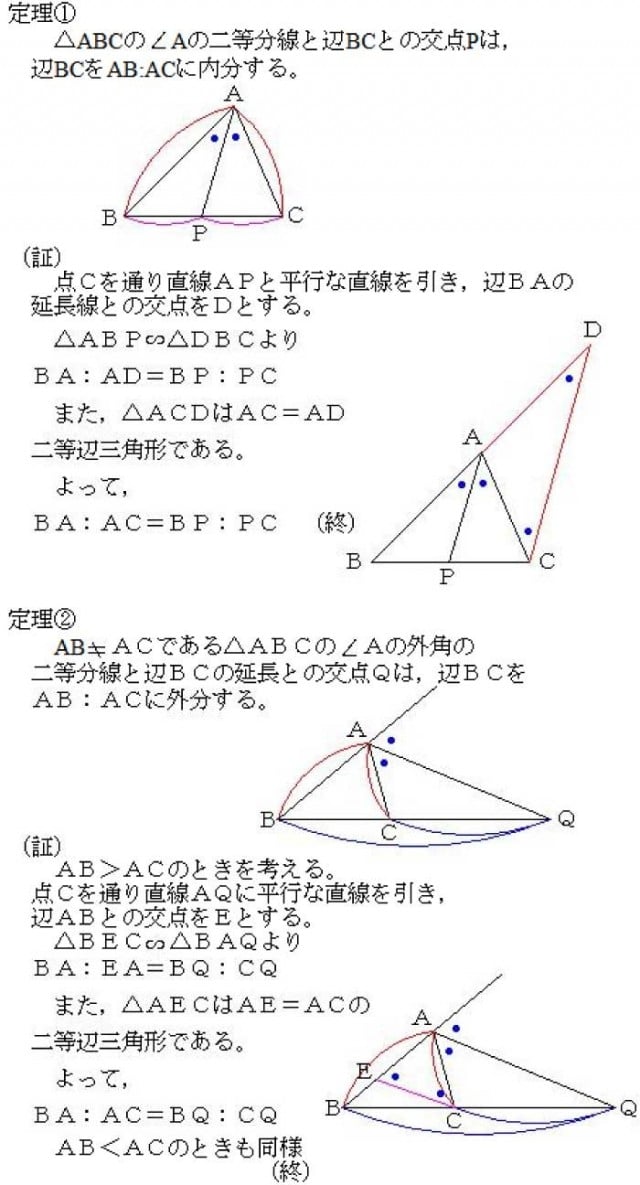
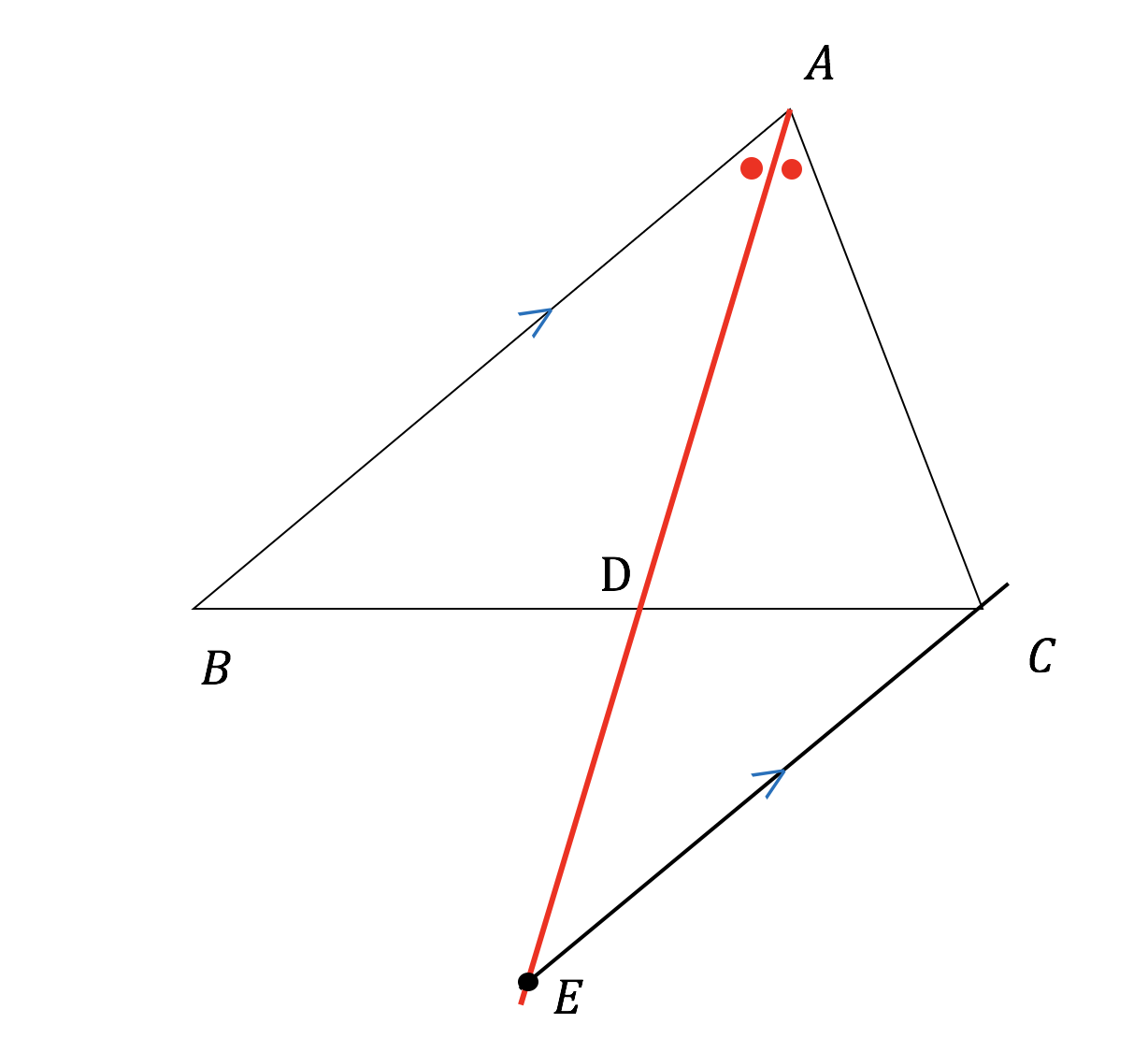
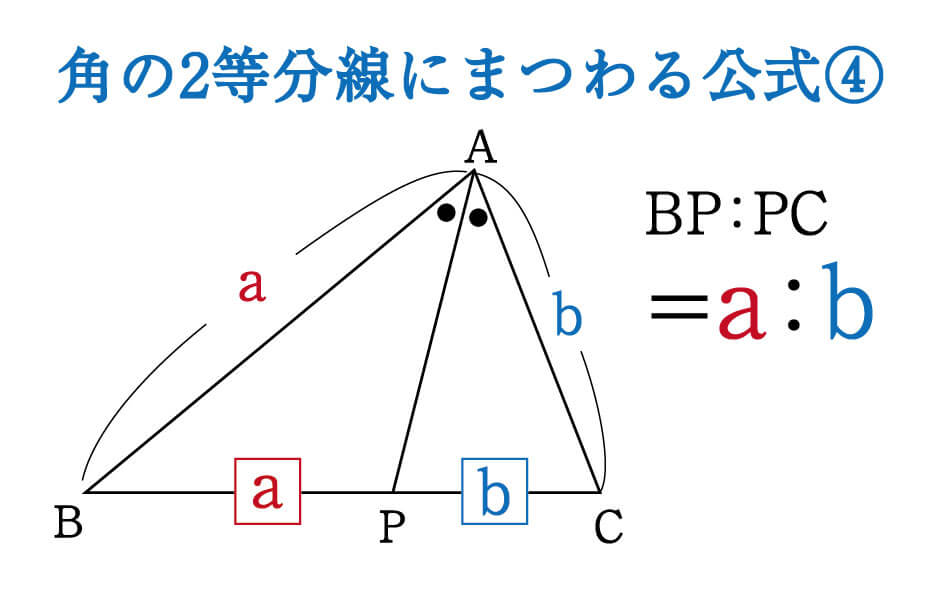
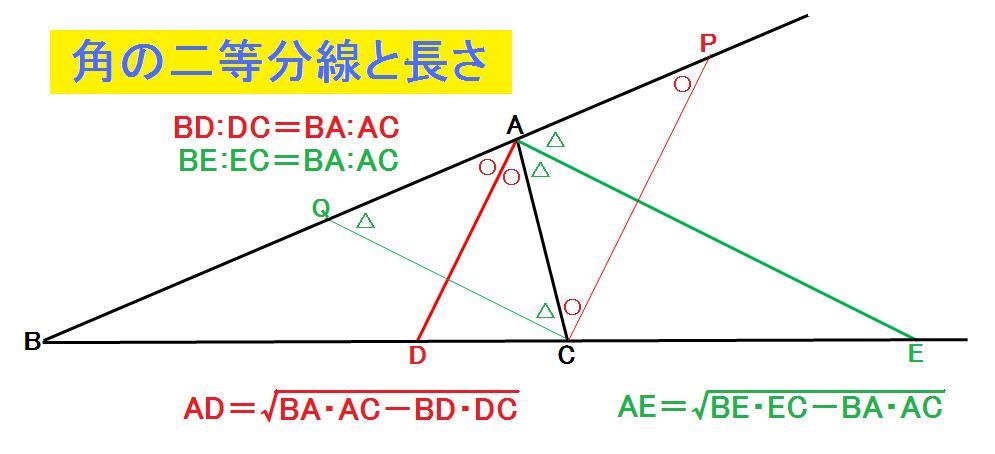
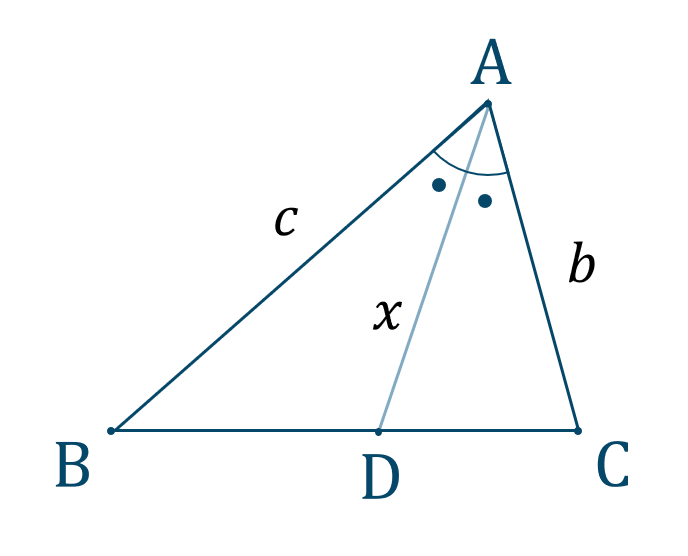
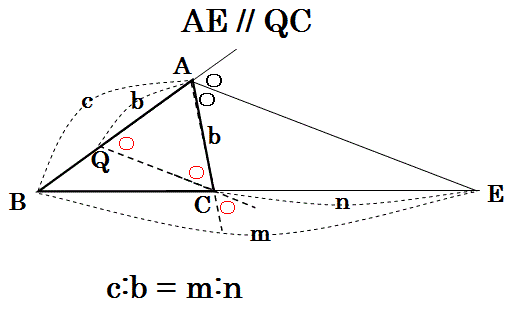
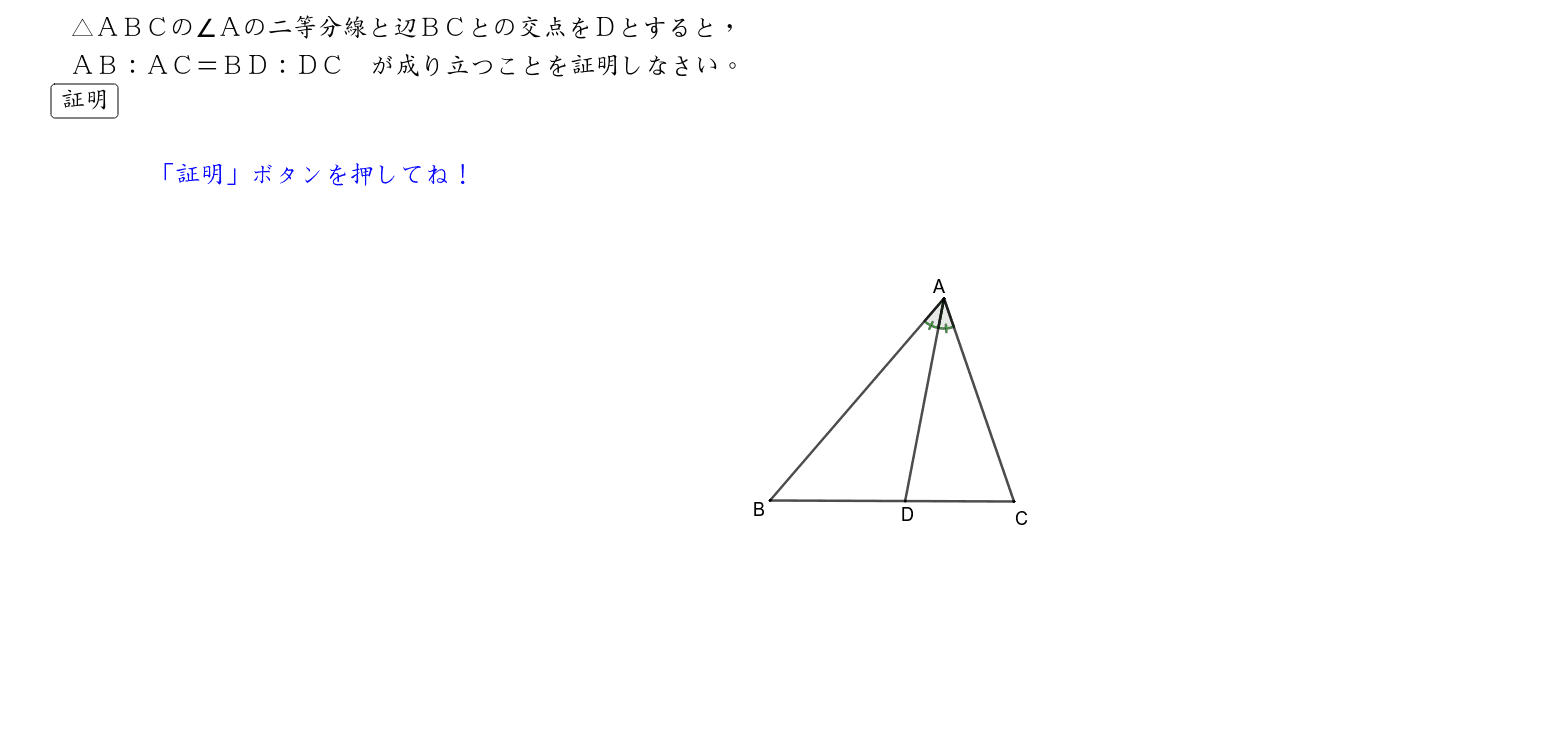
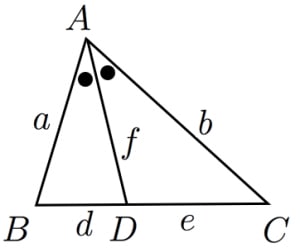
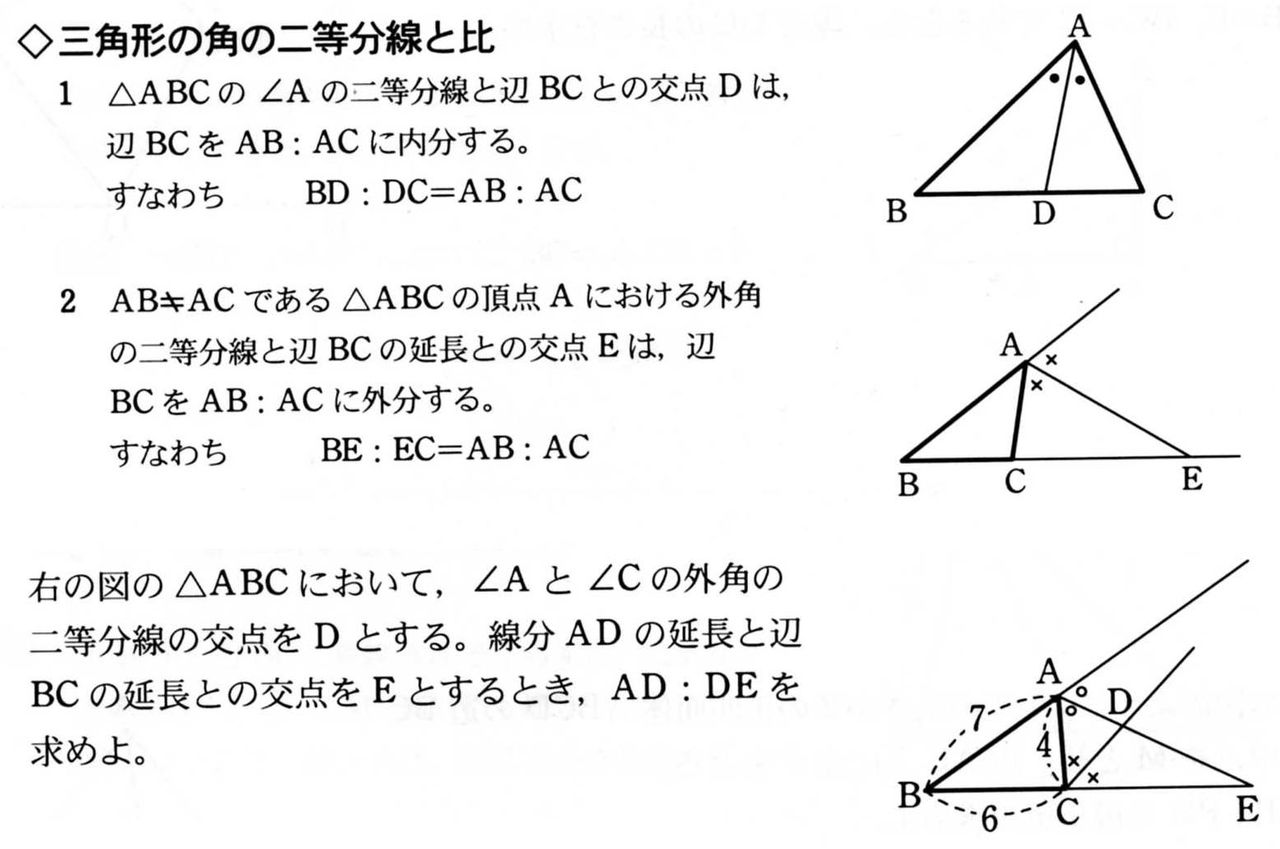
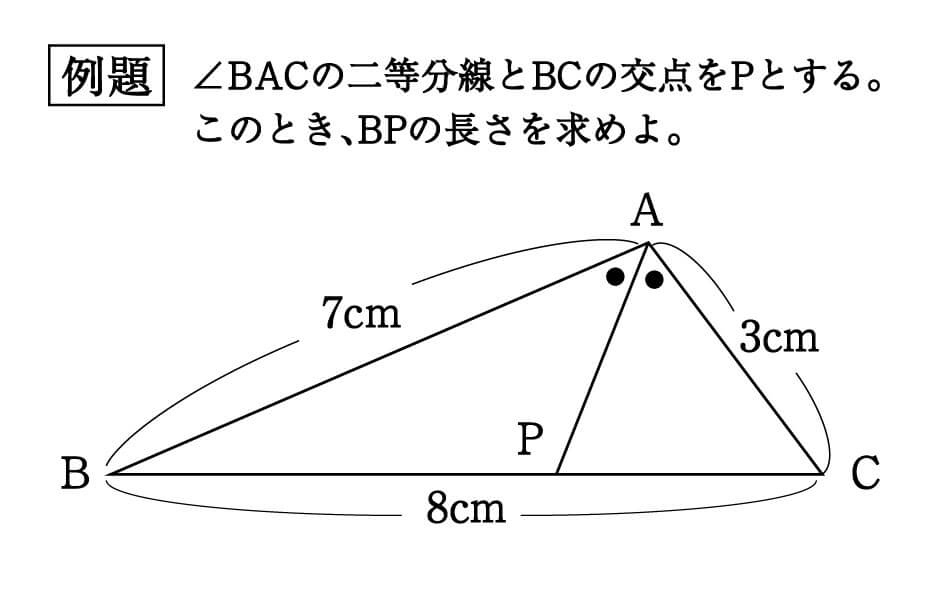
二等分線 辺の比- 高校数学A図形の性質角の2等分線と比まとめと問題 内角・外角の2等分線と比に関するまとめと問題です。 簡単な証明と確認問題があるので、基本から理解したい、問題の解き方を知りたいという方におすすめです。 目次 1 内角の2等分線と比 2内角の二等分線と辺の比の関係 から、 bp:pc=ab:ac が言えるね。つまり、 bp:3=8:6 だよ。この比例式より、 bp=4 と答えを出すことができるね。よって、辺bcの長さは、 bc=bppc=7 となる
二等分線 辺の比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  | |
 |  | |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  | |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  |  |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 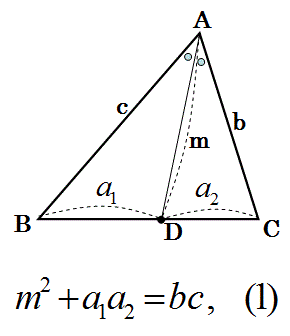 |
 |  | |
 |  | |
 |  | |
「二等分線 辺の比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
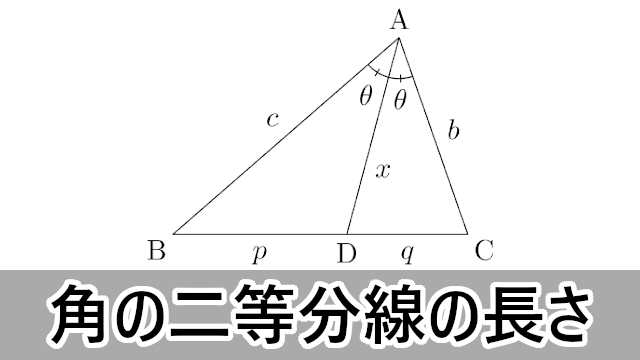 |  |
また,角 $\text{A}$ の二等分線と辺 $\text{BC}$ の交点を $\text{D}$ とするとき,$\text{AD}=15$ である。さらに,三角形 $\text{ABC}$ の内接円の半径は $4$ である。このとき以下の問いに答えよ。 (1) $\theta=\angle\text{BAD}$ とするとき $\sin\theta$ の値を求めよ。∠bacの二等分線と辺bcの交点をdとする。次の問いに答えよ。 ab=4,ac=10,bc=7のとき bdを求めよ。 a b c d ac=9,bd=3,dc=4 のときabを
Incoming Term: 二等分線 辺の比,
Komentar
Posting Komentar